稀代の妙問「モンティ・ホール問題」をコンピューターでシミュレートしてみた

知らない人だとほぼ全員が首をかしげる、人の直感と事実のズレまくっている妙な話なんですが、「モンティ・ホール問題」って知ってますか？

モンティ・ホール問題

これは、アメリカのショー番組でモンティ・ホールという司会者が行ったゲームの名前に由来しています。

モンティ・ホールゲームの内容

ゲームの内容はこういうものです。

1. プレイヤーの前には3つのドアがある
2. ドアの一つには景品が、残りの2つにはハズレのヤギが入っている。
3. プレイヤーはその中のドアの一つを選ぶ
4. すると、司会者が残りの2つのドアのうち、ハズレの方のドアを開ける
5. プレイヤーはもともと選んでいたドアか、残りもう一枚のドアかをもう一度選択する事ができる

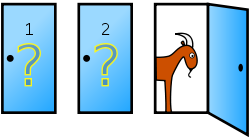
この時あなたがプレイヤーだったらどうしますか？

どちらを選ぼうとも確率は1/2だと思いませんか？

実はそうではないのが、この問題の面白いところなのです。

ということでシミュレーションプログラムを書いてみました。

#!/usr/bin/ruby</p> <p>@isChange @doors @playerDecide @mcOpenDoor @hit @count</p> <p>#① def InitialStatus(isChange) @isChange = isChange @playerDecide = 0 @mcOpenDoor = 0 @hit = 0 @count = 0 end</p> <p>#② def InitialDoors() random = rand(3)+1 case random when 1 @doors = [true, false, false] when 2 @doors = [false, true, false] when 3 @doors = [false, false, true] end p @doors end</p> <p>#③ def DecideDoor() @playerDecide = rand(3)+1 print("Player decided = ", @playerDecide, "\n") end</p> <p>#④ def MCOpenDoor(playerDecidedDoorNumber) random = rand(3)+1 while(playerDecidedDoorNumber == random || @doors[random-1] == true) print("redo = ", random, "\n") random = rand(3)+1 end @mcOpenDoor = random print("MC Opened door is = ", random, "\n") end</p> <p>#⑤ def PlayerOpenDoor(mcOpenedDoorNumber, playerDecidedDoorNumber) finalAnswer = 0 if(@isChange) finalAnswer = 6 - (mcOpenedDoorNumber + playerDecidedDoorNumber) else finalAnswer = playerDecidedDoorNumber end return finalAnswer end</p> <p>#⑥ def JudgeHit(finalAnswer) result = false if @doors[finalAnswer-1] == true @hit=@hit+1 result = true end @count=@count+1 return result end</p> <p>#条件初期化 true...変更志向 false...固定志向 InitialStatus(false)</p> <p>for num in 1..10000 do #ドアの初期化 InitialDoors()</p> <pre><code>#プレイヤーが最初にドアを選ぶ DecideDoor() #MCがドアをオープンする MCOpenDoor(@playerDecide) #プレイヤーのファイナルアンサー #変更志向なら余ったドアを選ぶ、そうでなければ最初に選んだドアを選ぶ finalAnswer = PlayerOpenDoor(@mcOpenDoor, @playerDecide) print("Player final-answer is = ", finalAnswer, "\n") #当たり判定 if JudgeHit(finalAnswer) p "Hit!" else p "Failed!" end

end

#最終結果表示

#試行回数 print("Test count = ",@count , "\n") #当たり回数 print("Hit count = ",@hit , "\n")

winrate = @hit.to_f / @count.to_f * 100 print("Winning rate = ",winrate , "%\n")

人間にわかりやすい感じを意識して書いてみました。

簡単に説明させていただきます～。

①部分

条件の初期化をしています。

②部分

ランダムに１～３の数字を出し、それに合わせて3枚のドアのうち、どれに景品があるのかを設定しています。

③部分

プレイヤーが最初にどのドアを選ぶかをランダムに決定しています。

④部分

司会者が、プレイヤーが選んだドア以外のはずれのドアをオープンします。

⑤部分

プレイヤーが最終的にどのドアを開くかを決定しています。 ドアチェンジをする設定だと、プレイヤーが最初に選んだドアと司会者が開けたドア以外の余った最後のドアを開きます。 ドアチェンジをしない設定だと、プレイヤーは最初に選んだドアを開きます。

⑥部分

当たり判定をしています。

その後、下の部分では、上の説明させていただいた部分のパーツを順次実行してゲーム全体の流れを作っています。

さらに最下部では、試行回数と、プレイヤーがゲームに勝利した回数を表示して、勝率を表示します。

ではコンピューターに1万回ゲームをやってもらいましょう。

実行してみますよー。ポチッとな。

・・・はい！3秒位で結果がでました。

まずこちら、プレイヤーが自分の最初の決定のままドアを変更しなかったパターン。

次にこちら、プレイヤーが司会者のドアオープン後にドアを変更したパターン。

ややや！

ドアを変更しなかったパターンに比べて勝率が2倍程度になっていますね！！

ということで正解は・・・

ドアを変更する方が有利になるというものでした。

不思議ですね。

これを説明するにはもっとドアの数を増やすとわかりやすいんですが、例えばドアが100枚になったとしましょう。

ルール通りにプレイヤーが最初にドアを選びます。

そして司会者が、プレイヤーが選んだドア以外、アタリのドア一枚を除いて、その他98枚のハズレのドアをすべて開け放ちます。

その時プレイヤーは最初に選んだドアで勝負をかけたほうがいいでしょうか、変更した方がいいのでしょうか？という事です。

アメリカの天才おばちゃんすごい

この問題にスポットライトが当たったのは、アメリカの超天才おばちゃん、「マリリン・ボス・サバント」さんのコラムに向けての一通の投書がきっかけでした。

モンティ・ホールの番組のゲームについて、ドアを変えたほうがいいのか、そのままの方がいいのかを尋ねた人にたいしてマリリンさんは「ドアを変えた方が2倍勝率が高くなる」と答えたんですねえ。

この発言でアメリカの数学の博士などからも「んなワケないやろ、どっちも同じじゃ」と非難を受けまくったらしく、アメリカでは大変な騒ぎとなったらしいです。

コンピューターでシミュレートして解決

それで結局、コンピューターのプログラムで解析をしてみたらマリリンさんが正しかった事が認められたという事です。

コンピューターってこういう使い方ができるんですね〜。

モンティ・ホール問題についてもっと知りたいかたはこちらが詳しいですよ♪ モンティ・ホール問題 - Wikipedia

ちなみに、上で書いたのは僕が書いたプログラムですが、もっとプログラミングのうまい人が書くと、たったこれだけで同じシミュレーションが実現されます。

#!ruby</p> <p>def foo(change) n = 3 a = rand(n) s = rand(n) begin x = rand(n) end until x != s && x != a if change ss = s begin s = rand(n) end until s != x && s != ss end return s == a ? 1 : 0 end</p> <p>a = 100000.times.map{foo(true)}.inject(&:+) b = 100000.times.map{foo(false)}.inject(&:+)</p> <p>puts "rate: #{a.to_f / b.to_f}"

これは実行するとこの様に出力されます。

ドアを変更した場合、変更しなかった場合の何倍勝率が上がるかというシミュレーションですね。 コンピューターに10万回ゲームをプレイしてもらったあと、やはり2倍に近い値が出ています。

プログラムコード（命令文）が少なく、効率的にコンピューターに理解させている構成の為、10万回が一瞬で終わります。

いやー、書いたのは僕の友だちのDyama(dyama's page)くんなんですが、2016年Ruby大賞を獲る人のコードはやはり洗練されかたが違いますね。 勉強になりますわあ。

このように、プログラミングというのは書く人のクセや思想や目的で随分変わる、非常に自由度の高いパズルみたいなものなんですね～。

パズル好きな人には楽しい上に、習得してみると何かの役に立つかもしれませんよ♪

本日もG線上のきりんにおこしいただきありがとうございます。

マリリンさんは頭の良さもさることながら、人格的にも素晴らしい人で、僕はだいすきです。

それではまた♪